
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Достаточные условия точки перегиба.Содержание книги
Поиск на нашем сайте
ТЕОРЕМА 2. Пусть функция Доказательство. Применяем формулу конечных приращений два раза
где Так как
То есть, если производная
ТЕОРЕМА 3. Пусть функция Доказательство. По формуле Тейлора имеем
Отсюда получаем
Так как
АСИМПТОТЫ ОПРЕДЕЛЕНИЕ. Пусть функция
ПРИМЕР 1.
ОПРЕДЕЛЕНИЕ 2. Пусть функция Если существует асимптота, то при
ПРИМЕР 2.
Прямая
ПЕРВООБРАЗНАЯ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
ОПРЕДЕЛЕНИЕ. Пусть функция
ОПРЕДЕЛЕНИЕ. Пусть функция Аналогично определяются первообразные на полуинтервалах, неограниченных промежутках. ПРИМЕР. Первообразной функции
ЗАМЕЧАНИЕ. Одна и та же функция может быть первообразной разных функций, однако они могут отличаться только на концах промежутка.
ТЕОРЕМА. Если функция Доказательство. Пусть Пусть
ОПРЕДЕЛЕНИЕ. Совокупность всех первообразных функции
Свойства неопределенного интеграла 1. Так как
2. Пусть функция
Пусть функция 3. Если функции
По определению это означает, что
4. Пусть функция Пусть функция
|
||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 255; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.006 с.) |

 дифференцируема в точке
дифференцируема в точке  , дважды дифференцируема в окрестности точки
, дважды дифференцируема в окрестности точки  меняет знак при переходе через точку
меняет знак при переходе через точку 
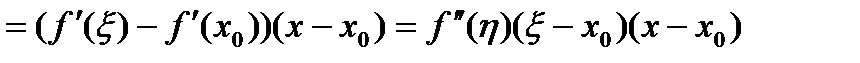 ,
,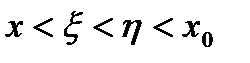 , если
, если 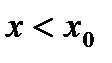 , и
, и  , если
, если 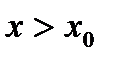 .
.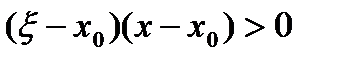 , то
, то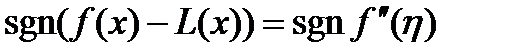 .
. меняет знак при переходе через точку
меняет знак при переходе через точку 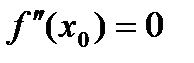 и
и  , тогда
, тогда 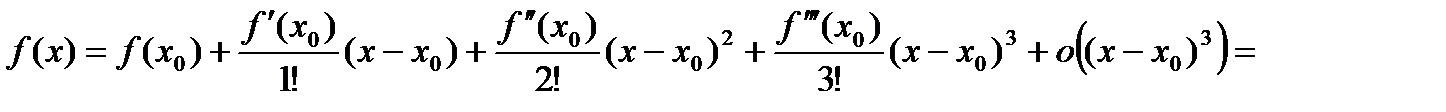
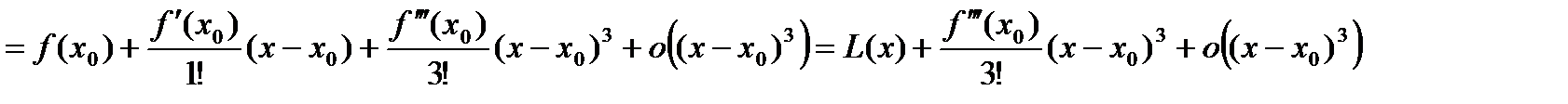 .
.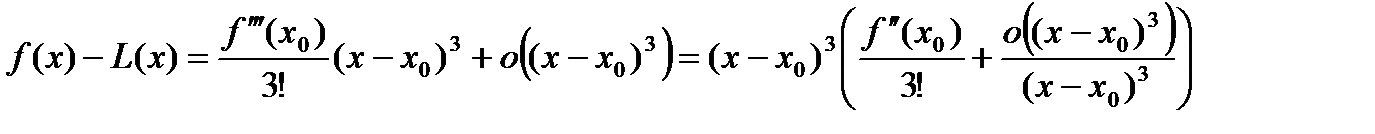

 выполняется неравенство
выполняется неравенство 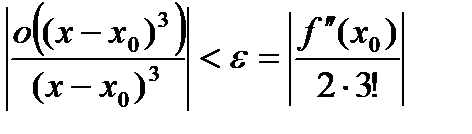 , то есть выражение
, то есть выражение  не меняет знак
не меняет знак 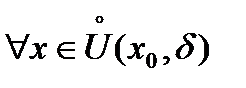 , то
, то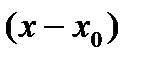 , то есть
, то есть  или
или 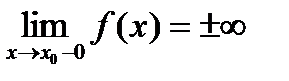 . Тогда прямая
. Тогда прямая  называется вертикальной асимптотой.
называется вертикальной асимптотой.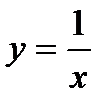 .
. 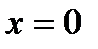 - вертикальная асимптота.
- вертикальная асимптота.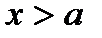 (
(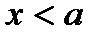 ). Если существуют числа
). Если существуют числа  такие, что
такие, что  при
при 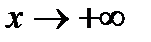 (
(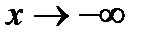 ), то прямая
), то прямая 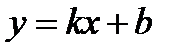 называется асимптотой графика функции
называется асимптотой графика функции 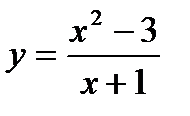 .
. ,
,  .
.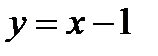 - асимптота графика при
- асимптота графика при  .
. определена на интервале
определена на интервале 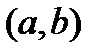 . Функция
. Функция 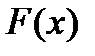 называется первообразной для функции
называется первообразной для функции 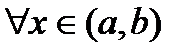
 .
.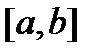 . Функция
. Функция 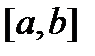 , если
, если 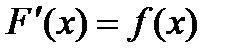 .
.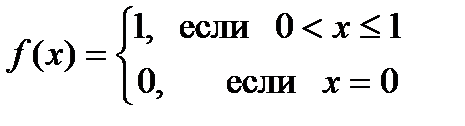 является функция
является функция 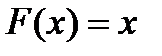 ,
, 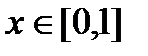 . Эта же функция будет первообразной для функции
. Эта же функция будет первообразной для функции 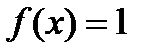 ,
, 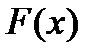 является первообразной функции
является первообразной функции  на интервале
на интервале 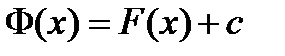 является первообразной функции
является первообразной функции 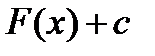 .
.
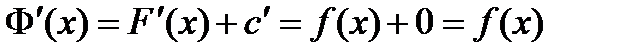
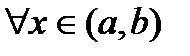 (функция
(функция 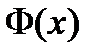 две первообразные функции
две первообразные функции 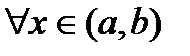 получаем
получаем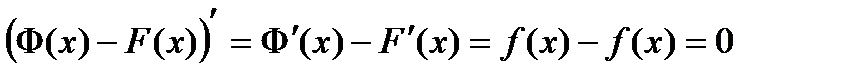 . По следствию из теоремы Лагранжа
. По следствию из теоремы Лагранжа 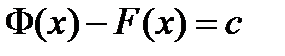
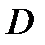 , называется неопределенным интегралом от функции
, называется неопределенным интегралом от функции  . Функция
. Функция  . Принято писать
. Принято писать 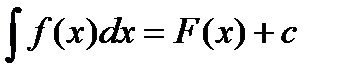 .
.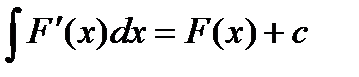
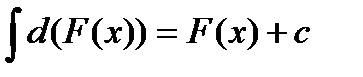 .
. , то получаем
, то получаем .
. 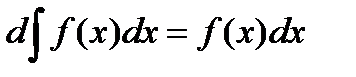 .
.
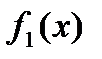 и
и  имеют на интервале
имеют на интервале  также имеет первообразную, причем
также имеет первообразную, причем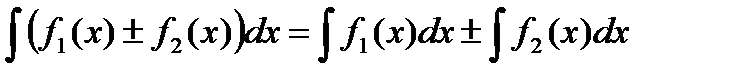 .
.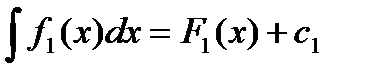 ,
, 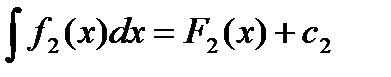 . Тогда
. Тогда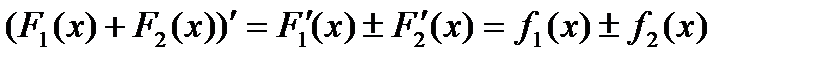 .
.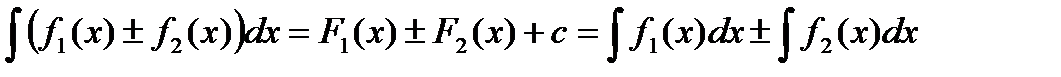 .
.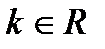 , тогда
, тогда  имеет первообразную, причем
имеет первообразную, причем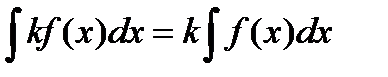 .
.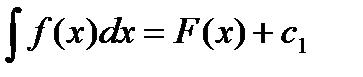 , тогда
, тогда 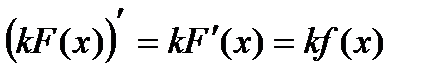 . По определению это означает
. По определению это означает .
.


