Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные теоремы теории вероятностей случайного событияСодержание книги
Поиск на нашем сайте Несовместными называются события, если их одновременное осуществление невозможно. Теорема сложения вероятностей: вероятность появления хотя бы одного (безразлично какого) события из нескольких несовместных событий равна сумме их вероятностей. Для двух событий имеем:
Пример 2. Найти вероятность выпадения «2» или «5» при бросании игрального кубика. Решение Событие A - выпадение «2», Событие B - выпадение «5», Тогда для события A или B по формуле теоремы сложения вероятностей получаем
Пример 3. В корзине находится 50 шаров: 10 белых, 20 черных, 5 красных и 15 синих. Найти вероятность появления белого или черного или красного шара при однократном изъятии шара из корзины. Решение Событие A - вынимание белого шара, Событие B - вынимание черного шара, Событие C - вынимание красного шара, По формуле сложения вероятностей имеем
Противоположным данному событию A называется такое событие В примере 3 противоположным событию Полной системой событий называется такая совокупность событий, которая содержит все возможные исходы испытаний, т.е. в результате испытаний появится хотя бы одно из них. Например, числа от «1» до «6» составляют полную систему событий при бросании игрального кубика. Сумма вероятностей событий, образующих полную систему, равна единице (для несовместных событий):
Теорема умножения вероятностей: вероятность одновременного наступления нескольких независимых событий равна произведению их вероятностей. Для двух событий имеем:
Пример 4. В одной корзине находится 5 черных и 10 белых шаров, в другой – 7 черных и 9 белых. Найти вероятность того, что при первом вынимании шаров из каждой корзины оба шара окажутся: а) черными; б) белыми; в) из первой корзины вынут черный шар, а из второй – белый; г) из первой корзины вынут белый шар, из второй – черный. Решение Событие A - вынимание черного шара из первой корзины, Событие B - вынимание белого шара из первой корзины, Событие C - вынимание черного шара из второй корзины, Событие D - вынимание белого шара из второй корзины, По формуле умножения вероятностей находим: а) б) в) из второй - белый; г) из второй - черный.
Все четыре возможных события, рассмотренные в данном примере, образуют полную систему событий, поэтому их сумма равна единице. Условной вероятностью случайного события B называется его вероятность при условии, что произошло какое-либо другое событие, например, A. Условная вероятность обозначается Вероятность события, состоящего из совместного появления двух зависимых между собой событий A и B (причем B зависит от того, произошло ли событие A) равна:
Пример 5. В коробке находятся 5 синих и 2 красных карандаша. Какова вероятность того, что последовательно один за другим будут вынуты красный и синий карандаши? Решение Событие A - первым вынут красный карандаш, Событие B - после красного вынут синий карандаш, По формуле умножения вероятностей получаем:
Пусть в результате испытаний могут появиться несколько событий
Пример 6. Вероятность попадания в цель при стрельбе из трех орудий: Решение Вероятности событий, противоположных событиям
Глава 5
|
||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 120; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.006 с.) |

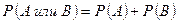 .
. ;
;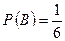 ;
;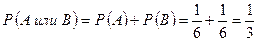 .
.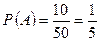 ;
; ;
;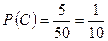 ;
; .
.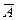 , которое заключается в том, что событие A не произошло. Сумма вероятностей противоположных событий равна единице:
, которое заключается в том, что событие A не произошло. Сумма вероятностей противоположных событий равна единице:  .
.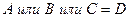 является вынимание синего шара, вероятность которого
является вынимание синего шара, вероятность которого  , и, таким образом,
, и, таким образом, 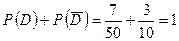 .
.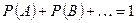 .
.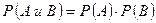 .
.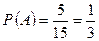 ;
;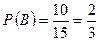 ;
; ;
;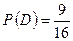 ;
;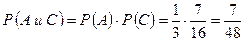 - оба шара окажутся черными;
- оба шара окажутся черными; - оба шара окажутся белыми;
- оба шара окажутся белыми;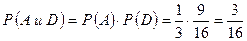 - из первой корзины вынут черный шар,
- из первой корзины вынут черный шар,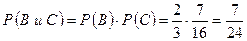 - из первой корзины вынут белый шар,
- из первой корзины вынут белый шар,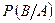 .
. .
. ;
; ;
;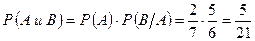 .
.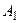 ,..,
,.., 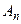 , причем вероятности появления каждого из события известны. Тогда вероятность появления хотя бы одного из этих событий равна разности между единицей и произведением вероятностей противоположных событий
, причем вероятности появления каждого из события известны. Тогда вероятность появления хотя бы одного из этих событий равна разности между единицей и произведением вероятностей противоположных событий 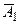 ,..,
,..,  :
: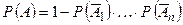 .
.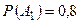 ,
, 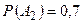 ,
,  . Найти вероятность хотя бы одного попадания (событие A) при одном залпе из всех орудий.
. Найти вероятность хотя бы одного попадания (событие A) при одном залпе из всех орудий.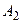 и
и 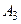 , соответственно равны
, соответственно равны 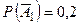 ,
,  ,
, 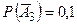 . Тогда искомая вероятность
. Тогда искомая вероятность  .
.