Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проекции скоростей двух точек твердого тела на прямую, соединяющую эти точки, равны друг другу.Содержание книги
Поиск на нашем сайте Тогда: VB= VA cosα /cosβ Угловая скорость и угловое ускорение одинаковы для всех точек тела. Угловую скорость ω можно найти, если определены проекции скоростей т. А, В на ось Y, перпендикулярную к оси X, которая проходит через т. А, В − VAY, VBY VAY=VAsinα; VBY= VB sinβ. Угловая скорость тела:
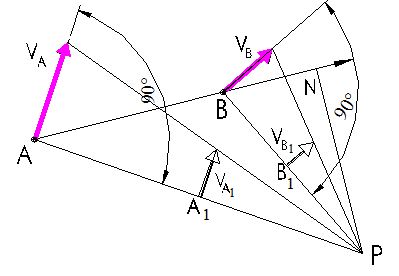
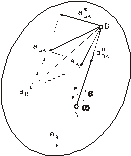
Мгновенный центр скоростей Скорость любой точки фигуры при ее плоском движении можно найти с помощью мгновенного центра скоростей (точки сечения, скорость которой в данный момент времени равна нулю). Пусть известна скорость т. А и направление скорости т. В при плоском движении твердого тела. Проведем перпендикуляры АР и ВР к направлениям скоростей точек А, В. Проекции скоростей точек, лежащих на линиях АР и ВР (например т. А1 и В1) на эти линии равны нулю. В точке пересечения этих линий скорость, проекции которой на две непараллельные оси равны 0, равна нулю.
Положение мгновенного центра скоростей определяется как точка пересечения перпендикуляров к векторам скоростей двух точек тела. Угловую скорость тела ω можно найти из соотношения.
здесь т. Р − мгновенный центр скоростей, АР и ВР − расстояния от точек до мгновенного центра скоростей. После того как положение мгновенного центра скоростей (т. Р) найдена, скорость любой точки тела определяется как вращательная скорость вокруг т. Р:
OX и OY. Скорость т. А − vА задана. Найти скорость точки В. Решение. Поскольку направления
Примерами плоского движения являются движение шатуна кривошипно-шатунного механизма и качение колеса. Пример 2. Определить скорость ползуна кривошипно-шатунного механизма в заданном положении при известной угловой скорости w кривошипа, длина которого OA = r Решение. 1. Кривошип ОА вращается вокруг т. О.
2. Шатун АВ совершает плоскопараллельное движение. Проекции скоростей т. А и В на линию, которая их соединяет равны:
3. Такой же результат получим при определении скоростей, используя мгновенный центр (МЦС). Проведем линии АР, ВР перпендикулярно направлениям скоростей в этих точках. Точка их пересечения является МЦС. Угловая скорость звена АВ
vB= vA BP/ AP В прямоугольном треугольнике АРВ угол АРВ 30° и BP/ AP =1 / cos 30°
Лк 2 КУ Лк 3 Ускорения точек твердого тела при его плоскопараллельном движении Ускорение любой точки плоской фигуры при ее плоском движении равно геометрической сумме ускорений полюса и ускорений точек при вращении фигуры относительно полюса. Вращательное ускорение равно геометрической сумме нормального и касательного ускорений. Полное ускорение т. В равно векторной сумме ускорения т. А, а также нормального и тангенциального ускорений т. В относительно А
Вектор нормального ускорения направлен от т. В к т. А, а его модуль: аВАn= ωАВ2 АВ здесь ωАВ − угловая скорость тела. Вектор тангенциального ускорения т. В относительно А направлен перпендикулярно к АВ, а его модуль:
здесь ε − угловое ускорение. Таким образом, ускорение какой либо точки (например, точки В) твердого тела можно определить, если дано значениях ускорения полюса
где Нормальное (центростремительное) ускорение Тангенциальное (вращательное ускорение) перпендикулярно к нормальному и линии, соединяющей полюс с т. В
Решение. 1. Кривошип ОА вращается вокруг т. О, а его угловая скорость: ωОА= p n/ 30 == 10p с−1 Скорость т. А направлена перпендикулярно к радиусу ОА:
vA=6p м/с;
vBA= vB sin 30°= vA tg 30°=3,464p м/с Ускорение т. В:
В уравнении (1) известны направления всех векторов, легко определить модули ускорений аА, аВАn. Ускорение аВ направлено по направляющей также как и скорость т. В. Нормальное ускорения аВАn − от т. В к А, а тангенциальное перпендикулярно к АВ. 1. Нормальное ускорение т. А аАn= ω2ОА ОА= 60 p2 м/с2; т. к. ω=const; ε=0; а А τ= 0. Полное ускорение а А =аАn и направлено от т. А к центру вращения в т. О. 2. Угловая скорость звена АВ ωАВ= vBA / ВА AB=1,039 м; ωАВ= 3,33p м/с 3. Нормальное ускорение т. B относительно А: аВАn= ω2АВАВ= 10,39 p2 м/с2
звена АВ. Модули ускорений аВ, аВАτ определим, проектируя левую и правую части уравнения (1) на оси координат X, Y: аВ cos 30°=аВАn аВ sin 30°=аА −аВАτ
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 319; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.006 с.) |

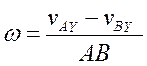
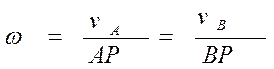
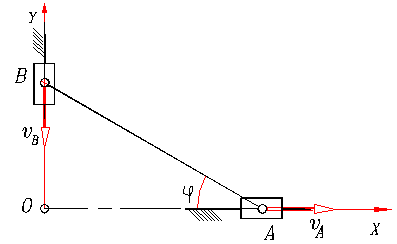 Пример 1. Линейка эллипсографа шарнирно соединена с ползунами А, В, которые перемещаются по прямолинейным напрвляющим
Пример 1. Линейка эллипсографа шарнирно соединена с ползунами А, В, которые перемещаются по прямолинейным напрвляющим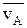 и
и  известны, то проектируя их на АВ, согласно теореме о проекциях скоростей, получим:
известны, то проектируя их на АВ, согласно теореме о проекциях скоростей, получим: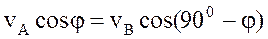 ;
; 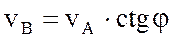 .
. Скорость т. А направлена перпендикулярно к радиусу ОА:
Скорость т. А направлена перпендикулярно к радиусу ОА: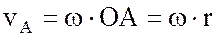
 ОА.
ОА.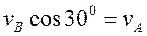 ;
; 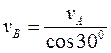
 ωАВ= vA/ AP= vB/ BP
ωАВ= vA/ AP= vB/ BP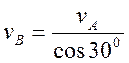
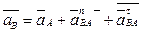
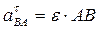
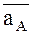 , известны угловая скорость w и угловое ускорение e тела. В некоторых случаях вместо углового ускорения могут использоваться данные о направлении ускорения в т. В или одной, например, тангенциальной, составляющей.
, известны угловая скорость w и угловое ускорение e тела. В некоторых случаях вместо углового ускорения могут использоваться данные о направлении ускорения в т. В или одной, например, тангенциальной, составляющей.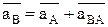 ,
,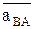 - ускорение точки В при вращении вокруг точки А:
- ускорение точки В при вращении вокруг точки А: 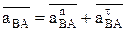 .
.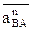 направлено от точки В к полюсу А,
направлено от точки В к полюсу А, 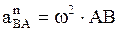 .
. АВ, а его величина:
АВ, а его величина: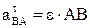
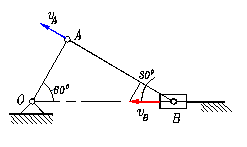 . Пример. Определить ускорение т. В кривошипно-шатунного механизма в заданном положении. Кривошип ОА длиной 0,6 м делает n=300 об./мин.
. Пример. Определить ускорение т. В кривошипно-шатунного механизма в заданном положении. Кривошип ОА длиной 0,6 м делает n=300 об./мин.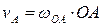
 ОА.
ОА.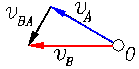 Скорости точек тела можно определить графически, если откладывать векторы скоростей в масштабе в соответствии с их направлением.
Скорости точек тела можно определить графически, если откладывать векторы скоростей в масштабе в соответствии с их направлением.
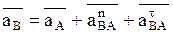 (1)
(1)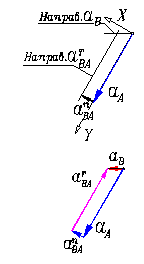 4. Выберем направление координатной оси Y таким образом, чтобы оно совпадало направлением звена АО, направление оси X тогда будет совпадать с направлением
4. Выберем направление координатной оси Y таким образом, чтобы оно совпадало направлением звена АО, направление оси X тогда будет совпадать с направлением