Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи лин и нелин программированияСодержание книги Поиск на нашем сайте Если ЗМП целев ф-ция f(x) и все ограничения f(
х, у- переменные в общем случае ЗЛП м. записаться в виде: найти max(min) { от ограничения типа неравенств можно перейти к огран типа рав-ва и наоборот, введением дополнит переменных.Тогда общ задачу ЛП можно записать: min
иногда ЗЛП записывают стандарт форме. З-чу нах-ия max цел. ф-ии м. свести к min ф-ции: min[-
ограничение ЗЛП образует некотор общую часть Н-мерного простр-ва, кот наз-ся многогранником решения. Задача дискретного программирования Быстрое развитие эк- мат. м-дов сопровождается появлением больших кол-ва нов проблем, кот делятся на 2 группы: 1) вычислительные, вызванные дискретностью переменных, нелин-тью 2)М-дологич проблемы вызванные действием случ. факторов. Реш- нием з-ч нахожд. оптим реш-ний при наличии оптим факторов заним-ся стохастич. программирование f( ЗЛП записывается обычно: max(min) при Данная з-ча яв-ся ЗДП, еслиG- дискрет множество, сущ 3 осн фактора ЗДП: 1) неделимость некоторых р-рсов(здания, машины) 2) логические отношения и связи 3) з-чи не яв-ся дискретными, но сводятся к ним. Имеется 3 основных метода реш-ия ЗДП: 1. отсечение 2. комбинаторные методы 3 приближенные методы. Задачи матем программир-я (ОПТИМИЗАЦИИ. программ) Задача оптим. яв-ся одним из важнейших задач экон. и управ пр-вом,процессов и т.д. Решение задачи оптимизации может разбиться на 3 этапа: 1) построение матем. модели; 2) нахождение оптим решения одним из метод матем программ. 3) практическ. использ-е результата решения. Оптимизация - целенаправленное деят-ность запл- щийся в получение наилучщих результатов при соответст условиях. На языке матиматики целевой ф-ции наилучщие результаты нахождения max и min. Управление – принятие решения о наиболее целесообразных действиях. Решение сложных соц- эк задач м-дами систем анализа в конечн. счете сводится к решению некоторой задачи оптимизации. В общем случае з-ча матем. прогр-ия: max(min)
ЗНП и методы его решения имеется з-ча max(min) { если хотя бы одна из ф-ий яв-ся нелин, то з-ча наз-ся ЗНП. Для решения з-чи НП не сущ-ет станд. методов реш-ия. Выбор метода решения зависит от содержания з-чи и опыта исследователя.М-д ЗНП может быть охарактеризована как многошаговые или как методы послед-го улучшения исходного решения.
Начальное значение
При решение задачи возникает 2 трудности: 1) выбор подходящих начальных значений 2) глобальный экстремум Эффективность методов ЗНП опред-ся след св-ми: - точность в поисках -надежность метода - скорость сходимости (к) Условные и безусловные ЗНП Если в системе или в уравнении отсутствует ограничения, то задача наз-ся з-чей безусловной оптимизации. Безусловная задача решается легче,чем условная з-ча, поэтому наряду с прямым методом решения услов задач часто применяется метод преобразования условных задач в бузуслов оптимизации, путем введения штрафных ф-ций. метод является одним из эффективных методов, позволяющих решать много задач оптимизации (найти глобальный экстремум). сущность метода: объект исследования и анализа не сама ц.ф., а некоторая другая функция Ψ(L), образуемая в результате преображения ф. f( если ц.ф.. f(
Метод штрафных функций
В кач-ве штраф. ф-ии можно взять функцию
Алгоритм решения задачи min f 1) выбир нач точку 2) при k=1,2,3,..., начиная с точки
Если на каждом шаге алгоритма удается найти глобальн min ф-цию Обычно
примечание. Если решается max(min) {
|
||
|
Последнее изменение этой страницы: 2017-01-23; просмотров: 433; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.009 с.) |

 заданы линейными ф-ями, то соотв задача наз-ся ЗЛП. Если хотя бы 1 из функций нелин, то это ЗНП.
заданы линейными ф-ями, то соотв задача наз-ся ЗЛП. Если хотя бы 1 из функций нелин, то это ЗНП. +
+  =
= 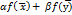 - полинома от многих переменных.
- полинома от многих переменных. - постоянные величины
- постоянные величины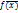 =
= 


 ,
, 
 ,
, 
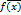 ]
]
 , f –целевая функция
, f –целевая функция - подмножества
- подмножества (
( (x)) i=
(x)) i= 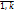


 =
=  , где к- номер шага итерации,
, где к- номер шага итерации,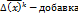 ,это шаг. к=0,1,2,3,4
,это шаг. к=0,1,2,3,4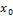 задается или выбирается. все сводится к нахождению
задается или выбирается. все сводится к нахождению 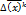 . Условие остановки
. Условие остановки 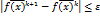
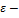 задан. точность решения задачи.
задан. точность решения задачи.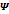 – преобразования
– преобразования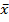 )
) является монотонно убывающей и ноль этой функции соотвествует значению max ц.ф. f(
является монотонно убывающей и ноль этой функции соотвествует значению max ц.ф. f(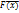 =f
=f 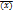 +
+ 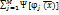 - безусловная задача оптимизации
- безусловная задача оптимизации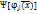 -штрафная ф-ия, путем добавления к целев. ф-ии одной или нескольких функций, учитывающие ограничения. Все условия учитываются в штраф. ф-иях.
-штрафная ф-ия, путем добавления к целев. ф-ии одной или нескольких функций, учитывающие ограничения. Все условия учитываются в штраф. ф-иях.
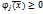 ,
, 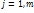 и
и 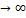 если это условие не выполняется.Поэтому если все условия выполняются, то min совпадает, а если не вып-ся, то добав шт ф-ций.
если это условие не выполняется.Поэтому если все условия выполняются, то min совпадает, а если не вып-ся, то добав шт ф-ций. ,
, 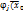 )>0,
)>0, 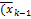 ) решается задача безусловной оптимизации, в результате определяется очередная точка
) решается задача безусловной оптимизации, в результате определяется очередная точка  )
)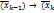 ) и т. д. процесс повторяется.
) и т. д. процесс повторяется.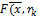 ) по x, то последовательность
) по x, то последовательность 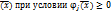 при
при 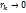
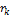 выбирают:
выбирают: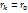 /
/ 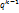 причем q>1- const,
причем q>1- const, 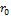 =[50;100]
=[50;100]