
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предмет теории вероятностей. Понятие случайного события.Стр 1 из 13Следующая ⇒
Предмет теории вероятностей. Понятие случайного события.
В различных разделах науки и техники нередко возникают ситуации, когда результат каждого из многих проводимых опытов заранее предугадать невозможно, однако можно исследовать закономерности, возникающие при проведении серии опытов. Нельзя, например, точно сказать, какая сторона монеты окажется сверху при данном броске: герб или цифра – но при большом количестве бросков число выпадений герба приближается к половине количества бросков. Исследование вероятностных закономерностей массовых однородных явлений составляет предмет теории вероятностей. Случайным событием (просто событием) называется любой факт, который в результате может произойти или не произойти. Элементы комбинаторики. Схемы выбора без возвращения и с возвращением.
При вычислении вероятностей часто приходится использовать некоторые формулы комбинаторики – науки, изучающей комбинации, которые можно составить по определенным правилам из элементов некоторого конечного множества. Определим основные такие комбинации.
Перестановки – это комбинации, составленные из всех п элементов данного множества и отличающиеся только порядком их расположения. Число всех возможных перестановок Рп = п!
Размещения – комбинации из т элементов множества, содержащего п различных элементов, отличающиеся либо составом элементов, либо их порядком. Число всех возможных размещений
Сочетания – неупорядоченные наборы из т элементов множества, содержащего п различных элементов (то есть наборы, отличающиеся только составом элементов). Число сочетаний
Урны и шарики Есть урна (то есть ящик), содержащая Рассмотрим следующие возможные схемы выбора: 1. Выбор с возвращением: каждый выбранный шарик возвращается в урну, то есть каждый из
2. Выбор без возвращения: выбранные шарики в урну не возвращаются, и в полученном наборе не могут встречаться одни и те же номера (выборка без повторений). И в том, и в другом случае результатом выбора является набор из 1. Выбор с учетом порядка: два набора номеров шариков считаются различными, если они отличаются составом или порядком номеров. Так, при выборе трех шариков из урны, содержащей 5 шариков, наборы 2. Выбор без учета порядка: два набора номеров шариков считаются различными, если они отличаются составом. Наборы, отличающиеся лишь порядком следования номеров, считаются одинаковыми. Так, в примере выше первые два набора Подсчитаем теперь, сколько же возможно различных результатов при каждой из четырех схем (выбор с возвращением и без, и в каждом из этих случаев учитываем ли мы порядок или нет). Теорема 2. Общее количество выборок в схеме выбора
и называется числом размещений из Доказательство. Первый шарик можно выбрать Следствие 1. Число возможных перестановок множества из Доказательство очевидно, если заметить, что перестановка есть не что иное, как результат выбора без возвращения и с учетом порядка всех Теорема 3. Общее количество выборок в схеме выбора
и называется числом сочетаний из Доказательство. Заметим, что, согласно следствию 1, из каждой выборки данного состава (состоящей из
То есть число выборок, различающихся еще и порядком, в Теорема 4. Общее количество выборок в схеме выбора
Доказательство. Первый шарик можно выбрать Теорема 5. Общее количество выборок в схеме выбора
Формула полной вероятности.
Определение 3.1. Пусть событие А может произойти только совместно с одним из событий Н 1, Н 2,…, Нп, образующих полную группу несовместных событий. Тогда события Н 1, Н 2,…, Нп называются гипотезами .
Теорема 3.1. Вероятность события А, наступающего совместно с гипотезами Н 1, Н 2,…, Нп, равна:
где p (Hi) – вероятность i- й гипотезы, а p (A/Hi) – вероятность события А при условии реализации этой гипотезы. Формула (3.1) носит название формулы полной вероятности. Доказательство. Можно считать событие А суммой попарно несовместных событий АН 1, АН 2,…, АНп. Тогда из теорем сложения и умножения следует, что
что и требовалось доказать.
Формула Бейеса.
Пусть известен результат опыта, а именно то, что произошло событие А. Этот факт может изменить априорные (то есть известные до опыта) вероятности гипотез. Например, в предыдущем примере извлечение из урны белого шара говорит о том, что этой урной не могла быть третья, в которой нет белых шаров, то есть р (Н 3/ А) = 0. Для переоценки вероятностей гипотез при известном результате опыта используется формула Байеса:
Действительно, из (2.7) получим, что 10. Формула (схема) Бернулли.
Рассмотрим серию из п испытаний, в каждом из которых событие А появляется с одной и той же вероятностью р, причем результат каждого испытания не зависит от результатов остальных. Подобная постановка задачи называется схемой повторения испытаний. Найдем вероятность того, что в такой серии событие А произойдет ровно к раз (неважно, в какой последовательности). Интересующее нас событие представляет собой сумму равно-вероятных несовместных событий, заключающихся в том, что А произошло в некоторых к испытаниях и не произошло в остальных п – к испытаниях. Число таких событий равно числу сочетаний из п по к, то есть
Локальная теорема Лапласа Использование формулы Бернулли при больших значениях
ВЕЛИЧИН Пусть непрерывная случайная величина Х задана плотностью распреде- ления f(х). Допустим, что все возможные значения X принадлежат отрезку [а;b]. Разобьем этот отрезок на п частичных отрезков длиной Δx1, 2 Δx,..., n Δx и выберем в каждом из них произвольную точку i x (i=1, 2,..., п). Определим математическое ожидание непрерывной величины по аналогии с дискретной; составим сумму произведений возможных значений i x, на вероятности попадания их в интервал i Δx:
Перейдя к пределу, получим определенный интеграл
Доказательство. График функции распределения F(x) случайной величины X, имеющей показательное распределение представлен на рисунке
Следствие. Для случайной величины, распределённой по показательному закону, математическое ожидание равно среднему квадратическому отклонению, т. е.
Показательный закон распределения играет большую роль в теории массового обслуживания и теории надёжности. Так, например, интервал времени Т между двумя соседними событиями в простейшем потоке событий имеет Неравенство Чебышева. Неравенство Чебышева, используемое для доказательства дальнейших теорем, справед-ливо как для непрерывных, так и для дискретных случайных величин. Докажем его для дискретных случайных величин.
Теорема 13.1(неравенство Чебышева). p( | X – M (X)| < ε) ≥ D (X) / ε². (13.1) Доказательство. Пусть Х задается рядом распределения
Так как события | X – M (X)| < ε и | X – M (X)| ≥ ε противоположны, то р (| X – M (X)| < ε) + + р (| X – M (X)| ≥ ε) = 1, следовательно, р (| X – M (X)| < ε) = 1 - р (| X – M (X)| ≥ ε). Найдем р (| X – M (X)| ≥ ε). D (X) = (x 1 – M (X))² p 1 + (x 2 – M (X))² p 2 + … + (xn – M (X))² pn. Исключим из этой суммы те слагаемые, для которых | X – M (X)| < ε. При этом сумма может только уменьшиться, так как все входящие в нее слагаемые неотрицательны. Для определенности будем считать, что отброшены первые k слагаемых. Тогда
D (X) ≥ (xk+ 1 – M (X))² pk+ 1 + (xk+ 2 – M (X))² pk +2 + … + (xn – M (X))² pn ≥ ε² (pk+ 1 + pk+ 2 + … + pn). Отметим, что pk+ 1 + pk+ 2 + … + pn есть вероятность того, что | X – M (X)| ≥ ε, так как это сумма вероятностей всех возможных значений Х, для которых это неравенство справедливо. Следовательно, D (X) ≥ ε² р (| X – M (X)| ≥ ε), или р (| X – M (X)| ≥ ε) ≤ D (X) / ε². Тогда вероятность противоположного события p( | X – M (X)| < ε) ≥ D (X) / ε², что и требо-валось доказать.
Теоремы Маркова и Бернулли.
Математическая статистика. Основные понятия. Математическая статистика занимается установлением закономерностей, которым подчинены массовые случайные явления, на основе обработки статистических данных, полученных в результате наблюдений. Двумя основными задачами математической статистики являются: - определение способов сбора и группировки этих статистических данных; - разработка методов анализа полученных данных в зависимости от целей исследования, к которым относятся: а) оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости от других случайных величин и т.д.; б) проверка статистических гипотез о виде неизвестного распределения или о значениях параметров известного распределения. Для решения этих задач необходимо выбрать из большой совокупности однородных объектов ограниченное количество объектов, по результатам изучения которых можно сделать прогноз относительно исследуемого признака этих объектов. Определим основные понятия математической статистики. Генеральная совокупность – все множество имеющихся объектов. Выборка – набор объектов, случайно отобранных из генеральной совокупности. Объем генеральной совокупности N и объем выборки n – число объектов в рассматривае-мой совокупности. Виды выборки: Повторная – каждый отобранный объект перед выбором следующего возвращается в генеральную совокупность; Бесповторная – отобранный объект в генеральную совокупность не возвращается.
Пусть интересующая нас случайная величина Х принимает в выборке значение х 1 п 1 раз, х 2 – п 2 раз, …, хк – пк раз, причем
Если исследуется некоторый непрерывный признак, то вариационный ряд может состоять из очень большого количества чисел. В этом случае удобнее использовать группированную выборку. Для ее получения интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько равных частичных интервалов длиной h, а затем находят для каждого частичного интервала ni – сумму частот вариант, попавших в i -й интервал. Составленная по этим результатам таблица называется группированным статистическим рядом:
Полигон и гистограмма. Для наглядного представления о поведении исследуемой случайной величины в выборке можно строить различные графики. Один из них – полигон частот: ломаная, отрезки которой соединяют точки с координатами (x 1, n 1), (x 2, n 2),…, (xk, nk), где xi откладываются на оси абсцисс, а ni – на оси ординат. Если на оси ординат откладывать не абсолютные (ni), а относительные (wi) частоты, то получим полигон относительных частот (рис.1). По аналогии с функцией распределения случайной величины можно задать некоторую функцию, относительную частоту события X < x. Определение 15.1. Выборочной (эмпирической) функцией распределения называют функцию F* (x), определяющую для каждого значения х относительную частоту события X < x. Таким образом,
где пх – число вариант, меньших х, п – объем выборки.
Замечание. В отличие от эмпирической функции распределения, найденной опытным путем, функцию распределения F (x) генеральной совокупности называют теоретической функцией распределения. F (x) определяет вероятность события X < x, а F* (x) – его относительную частоту. При достаточно больших п, как следует из теоремы Бернулли, F* (x) стремится по вероятности к F (x). Из определения эмпирической функции распределения видно, что ее свойства совпадают со свойствами F (x), а именно: 1) 0 ≤ F* (x) ≤ 1. 2) F* (x) – неубывающая функция. 3) Если х 1 – наименьшая варианта, то F* (x) = 0 при х ≤ х 1; если хк – наибольшая варианта, то F* (x) = 1 при х > хк. Для непрерывного признака графической иллюстрацией служит гистограмма, то есть ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высотами – отрезки длиной ni /h (гистограмма частот) или wi /h (гистограмма относительных частот). В первом случае площадь гистограммы равна объему выборки, во втором – единице (рис.2). Предмет теории вероятностей. Понятие случайного события.
В различных разделах науки и техники нередко возникают ситуации, когда результат каждого из многих проводимых опытов заранее предугадать невозможно, однако можно исследовать закономерности, возникающие при проведении серии опытов. Нельзя, например, точно сказать, какая сторона монеты окажется сверху при данном броске: герб или цифра – но при большом количестве бросков число выпадений герба приближается к половине количества бросков. Исследование вероятностных закономерностей массовых однородных явлений составляет предмет теории вероятностей. Случайным событием (просто событием) называется любой факт, который в результате может произойти или не произойти.
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 566; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.110.156 (0.063 с.) |
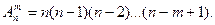 (1.4)
(1.4)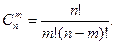 (1.5)
(1.5) занумерованных объектов, которые мы без ограничения общности будем считать шариками. Мы выбираем из этой урны
занумерованных объектов, которые мы без ограничения общности будем считать шариками. Мы выбираем из этой урны  шариков. Нас интересует, сколькими способами можно выбрать
шариков. Нас интересует, сколькими способами можно выбрать 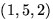 ,
,  и
и 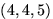 различны, если производится выбор с учетом порядка.
различны, если производится выбор с учетом порядка.
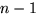 способом, и т.д. Последний
способом, и т.д. Последний  способом. По теореме 1, общее число способов выбора равно
способом. По теореме 1, общее число способов выбора равно 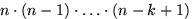 , что и требовалось доказать.
, что и требовалось доказать.
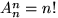

 выборок, отличающихся друг от друга только порядком элементов.
выборок, отличающихся друг от друга только порядком элементов. на
на 

 (3.1)
(3.1)
 (3.2)
(3.2) откуда следует справедливость формулы (3.2).
откуда следует справедливость формулы (3.2). , а вероятность каждого из них: pkqn-k, где q = 1 – p – вероятность того, что в данном опыте А не произошло. Применяя теорему сложения для несовместных событий, получим формулу Бернулли:
, а вероятность каждого из них: pkqn-k, где q = 1 – p – вероятность того, что в данном опыте А не произошло. Применяя теорему сложения для несовместных событий, получим формулу Бернулли: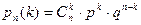 . (3.3)
. (3.3) требует выполнения арифметических действий над огромными числами, что обусловлено наличием факториалов в формуле для числа сочетаний. Поэтому, если число испытаний
требует выполнения арифметических действий над огромными числами, что обусловлено наличием факториалов в формуле для числа сочетаний. Поэтому, если число испытаний  ровно
ровно  раз применяют следующую теорему.
раз применяют следующую теорему. появления события
появления события  того, что событие
того, что событие  .
. приведены в специальной таблице. Для отрицательных значений аргумента пользуются той же таблицей и свойством четности функции
приведены в специальной таблице. Для отрицательных значений аргумента пользуются той же таблицей и свойством четности функции  , то есть
, то есть  .
.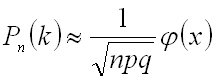 ,
, .
.


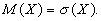






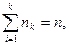 где п – объем выборки. Тогда наблюдаемые значения случайной величины х 1, х 2,…, хк называют вариантами, а п 1, п 2,…, пк – частотами. Если разделить каждую частоту на объем выборки, то получим относительные частоты
где п – объем выборки. Тогда наблюдаемые значения случайной величины х 1, х 2,…, хк называют вариантами, а п 1, п 2,…, пк – частотами. Если разделить каждую частоту на объем выборки, то получим относительные частоты 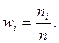 Последовательность вариант, записанных в порядке возрастания, называют вариационным рядом, а перечень вариант и соответствующих им частот или относительных частот – стати-стическим рядом:
Последовательность вариант, записанных в порядке возрастания, называют вариационным рядом, а перечень вариант и соответствующих им частот или относительных частот – стати-стическим рядом: Рис. 1.
Рис. 1. , (15.1)
, (15.1) Рис.2.
Рис.2.


