Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скалярное и векторное произведения
Скалярное произведение Из двух векторов
Это выражение называется скалярным произведением векторов Следовательно, По определению скалярное произведение обладает следующими свойствами: 1) 2) 3) Векторное произведение Из двух векторов
Модуль нового результирующего вектора находим по формуле:
Эта операция называется векторным произведением векторов Также общеизвестна формула
где Направление вектора
В терминах векторного произведения выражаются момент силы, момент импульса и др. Говоря о векторе, всегда имеем ввиду его компоненты. Вектор, в отличие от скаляра, определяется тремя числами. Поэтому такие операции как сложение, вычитание, скалярное и векторное произведения сводятся к привычным действиям с компонентами. Производная и интеграл Производная и ее применения Пусть функция у=f(х) определена в точках х и х1. Разность х1 - х называется приращением аргумента, а разность f(х1) - f(х) - приращением функции при переходе от значения аргумента х к значению аргумента х1. Приращение аргумента обозначают Если существует предел отношения приращения функции Операцию отыскания производной называют дифференцированием.
Cписок производных простейших элементарных функций 1.
2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
Если функции - Их сумма дифференцируема в точке х и - Произведение функций - Частное функций Первообразная и интеграл Пусть на интервале (а, b) задана непрерывная функция f(х). По определению функция F(х) называется первообразной функцией для f(х) на интервале (а, b), если на нем производная от F(х) равна f(х):
Очевидно, что если функция
Если F(х) какая-либо первообразная от f(х) на интервале (а, b), то возможные первообразные от f(х) на этом интервале выражаются формулой Неопределенным интегралом от непрерывной функции f(х) на интервале (а, b) называется произвольная ее первообразная функция. Неопределенный интеграл обозначается так:
Если
где С – некоторая постоянная.
Список основных неопределенных интегралов
1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
11.
12.
13.
14.
3.Задания для контрольной работы по дисциплине «Введениие в физику»
Основы векторной алгебры
1-1. Найдите а) модуль суммы б) разности в) скалярное произведение векторов г) косинус угла между векторами д) векторное произведение Решить задачу графически и аналитически.
1-2. Найдите а) модуль суммы б) разности в) скалярное произведение векторов г) косинус угла между векторами д) векторное произведение Решить задачу графически и аналитически.
1-3. Найдите а) модуль суммы б) разности в) скалярное произведение векторов
г) косинус угла между векторами д) векторное произведение Решить задачу графически и аналитически.
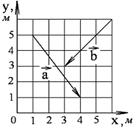
а) модуль суммы б) разности в) скалярное произведение векторов г) косинус угла между векторами д) векторное произведение Решить задачу графически и аналитически.
1-5. Найдите а) модуль суммы б) разности в) скалярное произведение векторов г) косинус угла между векторами д) векторное произведение Решить задачу графически и аналитически.
1-6. Найдите а) модуль суммы б) разности в) скалярное произведение векторов г) косинус угла между векторами д) векторное произведение Решить задачу графически и аналитически.
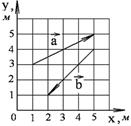
а) модуль суммы б) разности в) скалярное произведение векторов г) косинус угла между векторами д) векторное произведение Решить задачу графически и аналитически.
1-8. Найдите а) модуль суммы б) разности в) скалярное произведение векторов г) косинус угла между векторами д) векторное произведение Решить задачу графически и аналитически.
1-9. Найдите а) модуль суммы б) разности в) скалярное произведение векторов г) косинус угла между векторами д) векторное произведение Решить задачу графически и аналитически.
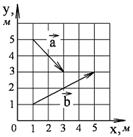
а) модуль суммы б) разности в) скалярное произведение векторов г) косинус угла между векторами д) векторное произведение Решить задачу графически и аналитически.
Прямая задача кинематики
|
||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 285; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.234.229 (0.094 с.) |
 и
и  можно образовать скаляр по правилу:
можно образовать скаляр по правилу: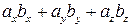
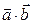 , или
, или 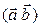 .
. .
.  =
= 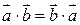 ,
,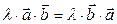 ,
,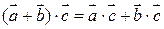
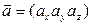 и
и 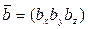 можно образовать новый вектор:
можно образовать новый вектор: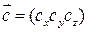 , где
, где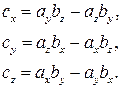
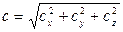 .
. или
или  .
.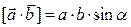 ,
, - угол между векторами
- угол между векторами  можно найти, используя следующий прием. Мысленно совмещаем продольную ось буравчика (правого винта, штопора) с перпендикуляром к плоскости, в которой лежат перемножаемые векторы (в данном примере – векторы
можно найти, используя следующий прием. Мысленно совмещаем продольную ось буравчика (правого винта, штопора) с перпендикуляром к плоскости, в которой лежат перемножаемые векторы (в данном примере – векторы 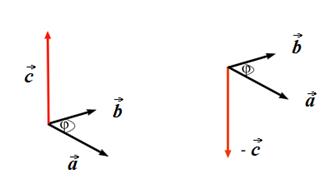
 , приращение функции обозначают
, приращение функции обозначают 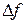 или
или 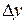 .
.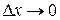 , то функция у=f(х) называется дифференцируемой в точке х, а этот предел называется значением производной функции у=f(х) в точке х и обозначается
, то функция у=f(х) называется дифференцируемой в точке х, а этот предел называется значением производной функции у=f(х) в точке х и обозначается 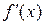 или
или 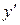 .
.
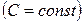
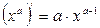 , а – любое число
, а – любое число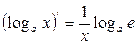 , в частности
, в частности 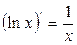
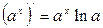 , в частности, при
, в частности, при 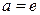 :
: 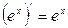

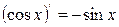
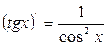
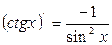
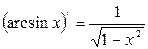
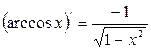
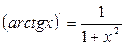

 и
и 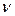 дифференцируемы в точке х, то:
дифференцируемы в точке х, то: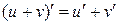 (теорема о дифференцировании суммы);
(теорема о дифференцировании суммы);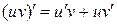 (теорема о дифференцировании произведения);
(теорема о дифференцировании произведения);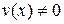 , и
, и 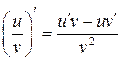 (теорема о дифференцировании частного).
(теорема о дифференцировании частного).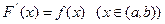
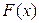 - первообразная для f(х) на (а,b), а С – некоторая постоянная, то функция
- первообразная для f(х) на (а,b), а С – некоторая постоянная, то функция  есть также первообразная для f(х), потому, что
есть также первообразная для f(х), потому, что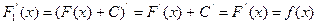
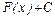 , где вместо С можно подставить любое число.
, где вместо С можно подставить любое число.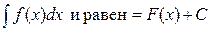 .
. ,
, 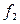 – непрерывные на интервале (а, b) функции и
– непрерывные на интервале (а, b) функции и  , и
, и 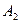 – постоянные, то имеет место следующее равенство, выражающее основное свойство неопределенного интеграла:
– постоянные, то имеет место следующее равенство, выражающее основное свойство неопределенного интеграла: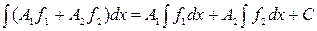 ,
,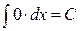 ;
;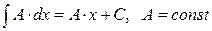 ;
;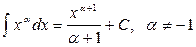 ;
;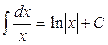 ;
;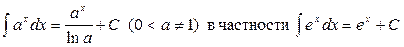 ;
;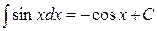 ;
;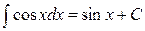 ;
;

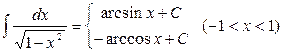 ;
;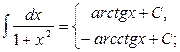
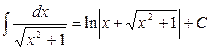 ;
;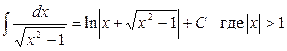 ;
;

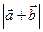

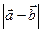 двух векторов
двух векторов 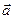 и
и 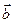 .
.
 1-4. Найдите
1-4. Найдите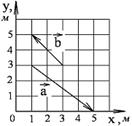
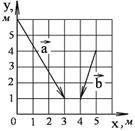
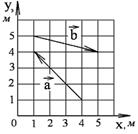 1-7. Найдите
1-7. Найдите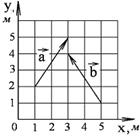
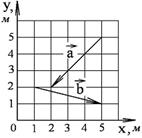
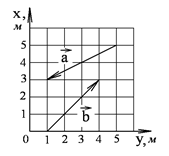 1-10. Найдите
1-10. Найдите