
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
При вращательном движении твердого тела под действием силы f работа равняется произведению момента этой силы на угол поворота.Содержание книги
Поиск на нашем сайте При вращательном движении твердого тела под действием силы F работа равняется произведению момента этой силы на угол поворота. Работа переменной силы при повороте тела на конечный угол равняется определенному интегралу от момента сил:
Покажем, работа, совершаемая под действием равнодействующего момента сил, равна изменению кинетической энергии тела. Действительно, dA = M·da = I·e·da = I·(dw/dt)·w·dt = I·d(w2/2), Произведя интегрирование по углу, получим: A12 = I·w22/2 - I·w12/2 = DEк. 2.Изменение кинетической энергии тела под действием силы Скалярная величина, равная половине произведения массы тела на квадрат его скорости называется кинетической энергией тела: Ek=(m*v^2)/2/ Кинетическая энергия тела (от гр. kinetikos — приводящий в движение) — это энергия, которой тело обладает вследствие движения. Eк = Smi·vi2/2 = Smi·(vi·vi)/2 = Полученное выражение представляет собой сумму трех слагаемых:
Кинетическая энергия твердого тела состоит из кинетической энергии его поступательного движения и энергии его движения E' относительно СО, связанной с центром масс. Теорема Кёнига справедлива для любого плоского движения при котором центр масс перемещается в некоторой фиксированной плоскости, а вектор угловой скорости все время перпендикулярен к этой плоскости. Примером плоского движения является качение. 3.Потенциальная энергия Единицей измерения энергии в СИ является Джоуль. Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии. Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения. Такие силы называются консервативными. Также потенциальная энергия является характеристикой взаимодействия нескольких тел или тела и поля. Любая физическая система стремится к состоянию с наименьшей потенциальной энергией. Потенциальная энергия упругой деформации характеризует взаимодействие между собой частей тела. Потенциальная энергия в поле тяготения Земли вблизи поверхности приближённо выражается формулой: Ep = mgh, где Ep — потенциальная энергия тела, m — масса тела, g — ускорение свободного падения, h — высота положения центра масс тела над произвольно выбранным нулевым уровнем. 4.Свойства потенциальной энергии. Вывод Момент инерции, по определению:
Радиус-вектор
где
Вынося за сумму
Поскольку старая ось проходит через центр масс, то суммарный импульс тела будет равен нулю:
Тогда:
Откуда и следует искомая формула:
где JC — известный момент инерции относительно оси, проходящей через центр масс тела. Момент силы, действующей на материальную точку. Пусть частица A движется произвольным образом относительно точки О под действием силы F (см. рис. 6.2). Моментом силы частицы относительно закрепленной точки называется величина, равная векторному произведению: M = [ r · F ], (6.3)
кинетическая энергия твердого тела при вращательном движении. Кинетическая энергия твердого тела складывается из кинетических энергий его частей Ei. Рассчитаем значение Ei для элементов твердого тела. Ei = mi·vi2/2 = mi·w2·ri2/2. Кинетическая энергия твердого тела будет равна: Eк = w2/2·Smi·ri2 = I·w2/2. (8.13) Заметим, что формула для расчета Eк похожа на выражение для определения кинетической энергии поступательного движения тела, только роль меры инертности в этом случае играет момент инерции, а не масса и характеристикой движения является угловая, а не линейная скорость твердого тела. Момент импульса
где Для нескольких частиц момент импульса определяется как (векторная) сумма таких членов:
где (В пределе количество частиц может быть бесконечным, например, в случае твердого тела с непрерывно распределенной массой или вообще распределенной системы это может быть записано как В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с. Из определения момента импульса следует его аддитивность: как, для системы частиц в частности, так и для системы, состоящей из нескольких подсистем, выполняется:
При вращательном движении твердого тела под действием силы F работа равняется произведению момента этой силы на угол поворота. Работа переменной силы при повороте тела на конечный угол равняется определенному интегралу от момента сил:
Покажем, работа, совершаемая под действием равнодействующего момента сил, равна изменению кинетической энергии тела. Действительно, dA = M·da = I·e·da = I·(dw/dt)·w·dt = I·d(w2/2), Произведя интегрирование по углу, получим: A12 = I·w22/2 - I·w12/2 = DEк. 2.Изменение кинетической энергии тела под действием силы Скалярная величина, равная половине произведения массы тела на квадрат его скорости называется кинетической энергией тела: Ek=(m*v^2)/2/ Кинетическая энергия тела (от гр. kinetikos — приводящий в движение) — это энергия, которой тело обладает вследствие движения. Eк = Smi·vi2/2 = Smi·(vi·vi)/2 = Полученное выражение представляет собой сумму трех слагаемых:
Кинетическая энергия твердого тела состоит из кинетической энергии его поступательного движения и энергии его движения E' относительно СО, связанной с центром масс. Теорема Кёнига справедлива для любого плоского движения при котором центр масс перемещается в некоторой фиксированной плоскости, а вектор угловой скорости все время перпендикулярен к этой плоскости. Примером плоского движения является качение. 3.Потенциальная энергия Единицей измерения энергии в СИ является Джоуль. Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии. Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения. Такие силы называются консервативными. Также потенциальная энергия является характеристикой взаимодействия нескольких тел или тела и поля. Любая физическая система стремится к состоянию с наименьшей потенциальной энергией. Потенциальная энергия упругой деформации характеризует взаимодействие между собой частей тела. Потенциальная энергия в поле тяготения Земли вблизи поверхности приближённо выражается формулой: Ep = mgh, где Ep — потенциальная энергия тела, m — масса тела, g — ускорение свободного падения, h — высота положения центра масс тела над произвольно выбранным нулевым уровнем. 4.Свойства потенциальной энергии.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 296; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.007 с.) |

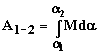 .
.
 — скалярная физическая величина, характеризующая способность некоего тела (или материальной точки) совершать работу за счет его нахождения в поле действия сил. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы[1]. Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином.
— скалярная физическая величина, характеризующая способность некоего тела (или материальной точки) совершать работу за счет его нахождения в поле действия сил. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы[1]. Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином.

 можно расписать как разность двух векторов:
можно расписать как разность двух векторов: ,
, — радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид:
— радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид:



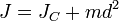 ,
,
 частицы относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:
частицы относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:
 — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта,
— радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта,  — импульс частицы.
— импульс частицы.
 — радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется.
— радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется. где
где  - импульс бесконечно малого точечного элемента системы).
- импульс бесконечно малого точечного элемента системы). .
.


