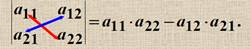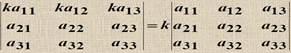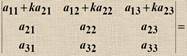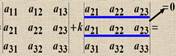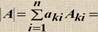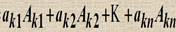Свойства алгебраических операций над матрицами

1) A+B=B+A (коммутативность),

2) (A+B)+C=A+(B+C) (ассоциативность).

матрицs A, B одинаковых размеров и любые числа S, t

1) (s t) A= s (t A); 2) s (A+B)= s A+ s B;

3) (s +t) A= s A+ t A.

Свойства операции умножения матриц:

1) (A B) C= A (B C) (ассоциативность),

2) A (B+C)=A B+ A C, (A+B) C= A C+ B C\(дистрибутивность),

3) t(A B)= (t A) B=A (t B).

Определители второго, третьего порядков и матрицы n-го порядка. Свойства определителей.

Определитель – это число. Обозн. Det A, |A|, D(A)

1) det (a ₁₁) = a ₁₁

2) Определители второго

3) Определители третьего с помощью метода треугольника.

Матрицы n-го????

Свойства определителей

1) Если в определителе есть нулевая строка (столбец), то он равен 0.

2) При перестановке двух строк (столбцов) определитель меняет знак

3) Определитель с двумя одинаковыми строками равен 0.

4)

5)

6)

7) Если одна из строк определителя есть линейная комбинация других строк, то определитель равен нулю.

8) Если к строке определителя прибавить линейную комбинацию других его строк, то определитель не изменится

9) Сумма произведений элементов какой-либо строки на соответствующие алгебраические дополнения другой строки равна нулю.

10) |A^T | = |A| 11) |AB|=|A| |B|

11) |AB| = |A| |B|

 

Алгебраическое дополнение и его свойства. Разложение определителя по строке

Алгебраическое дополнение A_{i j} = (-1) ^{i + j} M _{i j}

| a₁₁ a₁₂ ……a_1n |

Минор: M_IJ = | a₂₁ a₂₂ ……a_2n |

| …. … a_iJ …...|

| a_n1 a_{n2 …..} a_nn|

| a₁₁ a₁₂ ……a₁₃ | A₁₁= +(a₂₂ a₃₃- a₂₃ a₃₂)

|a₂₁ a₂₂ ……a₂₃ | A₁₂ = - (a₂₁ a₃₃ - a₂₃ a₃₁)

|a₃₁ a_{32 …..} a₃₃| A₁₃ = + (a₂₁ a₃₂ - a₂₂ a₃₁)

n

Определитель |A| = ∑a_1J A_1J= a₁₁ A₁₁ + a₁₂ A₁₂ ….. a_1n A_1n

J=1

Разложение определителя по k-ой строке

Присоединенная и обратная матрицы. Критерий обратимости.

Квадратная матрица A назыв-ся невырожденной, если |A|≠ 0, в противном случае матрица называется вырожденной

Квадратная матрица B называется обратной по отношению к матрице А того же порядка, если АB=BA=I. Обознач. A^-1.

Матрица А* называется присоединенной к матрице А, если в ее к-ой строке стоят алгебраические дополнения элементов к-ого столбца матрицы А.

Критерий обратимости. Для того чтобы существовала обратная матрица необходимо и достаточно, чтобы матрица была невырожденной

Док-во. Необходимость:

Det (A x A^-1) = det A x det A^-1= det I = 1 <═> det A ≠ 0

Достаточность: A x A^* = A^*x A D = Det A

|D 0 0 0 |

= |0 D 0 0 | = D x I = DxAx A^-1<═> A^-1 = 1/ detA x A^*

|0 0 D 0 |

|0 0 0 D |

 

5)Ранг матрицы как наивысший порядок ее миноров, отличных от нуля. Вычисление ранга матрицы с помощью элементарных преобразований.

Пусть в матрице A размера m x n выбраны произвольно k строк и k столбцов (k ≤ min(m, n)).

Элементы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную

матрицу порядка k, определитель которой называется минором k-ого порядка матрицы A.

Максимальный порядок r отличных от нуля миноров матрицы A называется ее рангом и

обозначается rang A.

Любой минор матрицы A порядка r = rang A называется базисным минором.

Строки и столбцы, на пересечении которых стоит базисный минор, называются соответственно базисными строками и базисными столбцами.

Если все элементы матрицы A равны нулю, то считается, что rang A= 0.

Теорема о базисном миноре.

Базисные строки (базисные столбцы) матрицы линейно независимы. Любая строка (любой столбец) матрицы является линейной комбинацией базисных строк (базисных столбцов).

Основным методом вычисления ранга матрицы является метод элементарных преобразований (метод Гаусса)

Операции, не меняющие ранга матрицы

1) Вычеркивание нулевой строки.

2) Вычеркивание одинаковых строк.

3) Перестановка строк.

4) Умножение строки на ненулевое число.

5) Прибавление к строке линейной комбинации других строк.

6) rang A ^Т = rang A.

7) rang (A × B)£min(rang A, rang B).

6)Система n линейных уравнений с n переменными (общий вид). Матричная форма записи системы. Совместные и несовместные, определенные и неопределенные системы

ОДНОРОДНЫЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ (ОСЛАУ).

Однородной системой m линейных алгебраических уравнений для n неизвестных

(1) { a₁₁x₁ + a₁₂x₂+……+ a_1n x_n = 0

{a₂₁x₁ + a₂₂ x₂ + … + a_2nx_n = 0

{ …………………………

{a _m1x₁ + a _m2 x₂ + … + a_mnx_n = 0 A × X =Q

 

(a₁₁ a₁₂ ……a_1n ) (x₁ ) столбец (0) нулевой

A = (a₂₁x₁ a₂₂ …a_2n) m × n – матрица X = (x₂) неизвестных Q = (0) столбец

………… ситемы (…) высоты n (..) высоты m

(a _m1 a _m2 … a_mn) (x _m) (0)

 

Система уравнений называется совместной, если она имеет хотя бы одно решение.

Система уравнений называется не совместной, если она не имеет решений.