Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные операции над матрицами. Св-ва операций.Стр 1 из 9Следующая ⇒
Матрицы. Основные понятия. Виды матриц. Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины (или n столбцов одинаковой длины). Место каждого эл-та определяется номером строки и столбца, на пересечении кот. он находится. Эл-ты матрицы обозначаются aij, где i – ном. строки матр., а j – ном. столбца матр. У матрицы есть 2 диагонали. Элементы, стоящие на диагонали, идущей из верхнего угла, образуют главную диагональ матр., а эл-ты стоящие на другой диагонали образуют вспомогательную диагональ матр. Матрица записывается в виде:
Мат-ца может состоять как из одной строки, так и из одного столбца. Мат-ца может состоять даже из одного эл-та. Мат-цы равны между собой, если равны все соответствующие эл-ты этих матриц, т. е. А = В, если aij = bij. Мат-ца А наз. симметричной, если она квадратная и если все aij = аji. Если m = n, то мат-ца называется квадратной. Кв. мат-цу размера "n×n" называют матрицей n - ого порядка. Кв. мат-цу, у кот. все эл-ты, кроме эл-ов глав. диагонали, равны нулю, наз. диагональной матрицей. Диаг-ая матрица:
Диаг-ая матрица, у кот. каждый эл-т глав.диагонали =1, наз. единичной матрицей. Единичная матрица:
Кв. матрица, называется треугольной, если все эл-ты матрицы, расположенные по одну сторону от глав. диагонали, =0. Матрица, все эл-ты кот=0, наз. нулевой матрицей и обозначается буквой О. В матричном исчислении матрицы О и Е играют роль 0 и 1 в арифметике. Матрица, содержащая 1строку или 1столбец, наз. вектором (Или вектор-строка, или вектор-столбец). Матрицу В называют т р анспонированнойматрицей А, а переход от А к В транспонированием мат-цы, если эл-ты каждой строки матрицы А записать в том же порядке в столбцы матрицы В. Обозначается АТ.
Другими словами, aij = bji. Линейные операции над матрицами. Св-ва операций. Равенство матриц Матрицы A = || ai j || и B = || ai j || считаются равными, если они имеют одинаковые размеры и их соответствующие матричные элементы попарно равны:
К линейным операциям над эл-ми множества или пространства относятся оп-ции сложения эл-ов и их умножения на скаляр (число). Умножение матрицы на число
Сложение матриц
Оп-ция сложения определена только для матриц одинаковых размеров. Результатом сложения матриц A = || ai j || и B = || bi j || явл. матрица C = || ci j ||, эл-ты кот. равны сумме соответствующих матричных эл-ов:
Линейной комбинацией матриц A и B наз.выражение вида Определители. Основные понятия. Свойства определителей. Квадр. матрице А порядка N можно сопоставить число det A (или |A|), называемое ее определителем следующим образом:
Определитель мат-цы А также наз. ее детерминантом. Методы, позволяющие реализовать вычисление определ-ей высоких порядков на основе определителей низших порядков. Один из методов основан на св-ве разложения определителя по элементам некоторого ряда. При этом заметим, что определ-ли невысоких порядков (1, 2, 3) желательно уметь вычислять согласно определению. Вычисление определ-ля 2-го порядка иллюстрируется схемой:
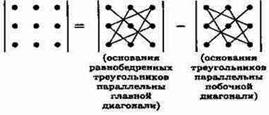
При вычислении определителя 3-го порядка удобно пользоваться правилом треугольников (или Саррюса):
Свойства определителей 1. Определитель не изменится, если его строки заменить столбцами, и наоборот. 2. При перестановке двух параллельных рядов определитель меняет знак 3. Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя. 4. Определитель, имеющий два одинаковых ряда, равен нулю. Из св-в 3 и 4 следует, что если все эл-ты некотор. ряда пропорциональны соответствующим эл-там параллельного ряда, то такой определитель равен нулю. 5.Вычисление определителей 2-го и 3-го порядков. Св-ва определит.(сумма опред., тождественные преобраз., сумма произвед. эл-ов строк и столбцов) Вычисление определ-ля 2-го порядка иллюстрируется схемой:
При вычислении определителя 3-го порядка удобно пользоваться правилом треугольников (или Саррюса):
Свойства определителей 1. Если эл-ты какого-либо ряда опред-ля представляют собой суммы 2х слагаемых, то опред-тель может быть разложен на сумму 2х соответствующих опред-лей.
2. Определитель не изменится, если к эл-там 1ого ряда прибавить соответствующие эл-ты параллельного ряда, умноженные на любое число.
3. Определитель произвед-ия 2х квадр. матр-иц: C=A*B равен произвед-ию detС= detВ* detА. 4. Сумма произвед-ий эл-ов строки или столбца,по кот. раскрывается опрделит. умноженный на алгебраич. дополнение параллельного столбца или строки равен нулю. Билет 7. Невырожденные матрицы. Обратная матрица. Основные понятия. Св-ва обр. матрицы. Алгоритм выч-ния обр. матрицы. Невырожденной матрицей называется квадратная матрица Понятие обратной матрицы вводится только для квадратных матриц. Если A – квадратная матрица, то обратной для неё матрицей называется матрица, обозначаемая A-1, если при умножении этой матрицы на данную, как справа, так и слева получается единичная матрица. Е – единичная матрица того же порядка, что и матрица А. Свойства обратной матрицы: 1. 2. 3. Для нахождения обратной матрицы 1.Найдем определитель матрицы А и убедимся, что он отличен от нуля, т.е. матрица А невырожденная и имеет обратную матрицу 2. Находим матрицу А’, транспонированную к А. 3. Находим алгебраические дополнения эл-тов транспонированной матрицы А’ij=Ail(i=1, 2…, n; j=1, 2…, n) и составляем из них присоединенную матрицу А: aij=A’ij=Aij(i=1, 2…, n; j=1, 2…, n). 4. Вычисляем обратную матрицу по формуле
Метод окаймляющих миноров Пусть в матрице A найден ненулевой минор n -го порядка M. Рассмотрим все миноры (n + 1)-го порядка, включающие в себя (окаймляющие) минор M; если все они равны нулю, то ранг матрицы равен n. В противном случае среди окаймляющих миноров найдется ненулевой, и вся процедура повторяется. 2. Метод элементарных преобразований Ранг матрицы равен числу ненулевых строк в матрице после приведения её к ступенчатой форме при помощи элементарных преобразований над строками матрицы.
Замечания 3.1 1. Один столбец 2. Любая часть системы столбцов называется подсистемой. Теорема о ранге матрицы. Ранг матрицы А равен максимальному числу линейно независимых столбцов (или равен рангу системы столбцов матрицы А). Доказательство. Пусть Системы линейных алгебраических уравнений (СЛАУ). Основные понятия. Матричная форма записи СЛАУ. Основные понятия: Ситемой линейных алгебраических уравнений, содержащих m уравнений и n неизвестных, называется система вида
Решением системы 1 называется n- значением: x1=c1, x2=c2, xn=cn, где сij= const, при подстановке которых в один, все уравнения обращаются в верные равенства.
b= c2 cn Cистема называется совместной, если она имеет хотя бы одно решение; и несовместной, если она не имеет решений.
Совместная система называется определенной, если она имеет единственное решение; и неопределенной, если она имеет более одного решения. Каждое решение будем называть частным решением. Совокупность частных решений образует общее решение. Решить систему означает выяснить, совместна она или нет. Если совместна, то найти общее решение. (aij), i = 1, m, называются коэффициентами j = 1, n системы bi- свободные члены,xi-неизвестное A x = B – матричная форма записи СЛАУ.
А=
Х=
b=
Две системы назыв. эквивалентными (равносильными), если они имеют одно и тоже общее решение,т.е. любое решение одной из них явл. Решением другой и наоборот. Замечание: Эквивалентные системы получаются в частности при элементарных преобразованиях системы и при условии, что преобразования совершаются лишь над строками матрицы. СЛАУ назыв. однородной, если все ее свободные члены равны нулю Замечание: однородная сист. Всегда совместна, поскольку существуют тривиальные решения: х1=о, х2=0, хm=0. СВОЙСТВА ОБРАТНОЙ МАТРИЦЫ 1) Если матрица Действительно, чтобы существовали произведения 2) Если обратная матрица существует, то она единственная. Действительно, если предположить, что существует две матрицы
то будет существовать и произведение
и Следовательно, 3) Если матрица
Действительно, так как
и, следовательно, Квадратная матрица, определитель которой отличен от нуля, называется невырожденной. Условие невырожденности матрицы Условие существования решения методом обратной матрицы.: Матрица
где
Матрица Решение ур-ий вида АХ = В, ХА = В, АХВ = С АХ = В, ХА = В, АХВ = С, где А,В,С — задаваемые матрицы, Х- искомая матрица. Билет 19.Модель межотраслевого баланса Леонтьева. Основные соотношения. Примеры задач. В 1930-е годы Василий Леонтьев применил метод анализа межотраслевых связей с привлечением аппарата линейной алгебры для исследования экономики США. Метод стал известен под названием «затраты — выпуск». Если матрица Е-А явл невырожденной (det -1 -1 не равен 0), то сущ-ет ей обратная Е-А. X=AX+Y; X-AX=Y; (E-A)*X=Y; X=(E-A) *Y (E-A= S); X=S*Y, где S-матрица полных затрат. Sij=xi- объем продукции. Пример расчета межотраслевого баланса Рассмотрим 2 отрасли промышленности: производство угля и стали. Уголь требуется для производства стали, а некоторое количество стали — в виде инструментов — нужно для добычи угля. Предположим, что условия таковы: для производства 1 т стали нужно 3 т угля, а для 1 т угля — 0,1 т стали.
Мы хотим, чтобы чистый выпуск угольной промышленности был Для производства Нужно дополнительно производить уголь и сталь, чтобы использовать их в другой отрасли. Обозначим x 1 — количество угля, x 2 — количество стали. Валовый выпуск каждой продукции найдем из системы уравнений:
Решение: 500 000 т угля и 100 000 т стали. Для систематического решения задач расчета межотраслевого баланса находят, сколько угля и стали требуется для выпуска 1 т каждого продукта.
x 1 = 1,42857 и x 2 = 0,14286. Чтобы найти, сколько угля и стали нужно для чистого выпуска Аналогично составляем уравнения для получения количества угля и стали для выпуска 1 т стали:
x 1 = 4.28571 и x 2 = 1.42857. Для чистого выпуска Валовый выпуск для производства Общее определение линейного пространства. Линейное векторное пространство. Примеры линейных пространств.
Умножение: λ*U, U Аксиомы (свойства) линейного пространства:
1) 2) 3) существует такой элемент 4) для любого 5) 6) 7) 8) Пример линейного пространства: Гильбертово пространство - пространство последовательностей со сходящимся рядом квадратов. Элементами (векторами) такого пространства являются бесконечные числовые последовательности x = (x1, x2,..., xn,...) такие, что ряд x21+ x22+... + х2n+... сходится. 24. n-мерное линейное векторное пространство. Размерность и базис векторного пространства. Разложение вектора по системе векторов. Переход к новому базису. n -мерное векторное пространство – пространство, имеющее n измерений (размерности n). Обычно этот термин применяется к пространству размерностью более трёх. При n=∞ имеем бесконечномерное пространство. Размерность векторного пространства -максимальное число линейно-независимых векторов в векторном (линейном) пространстве. Если это число конечно, то пространство называется конечномерным (многомерным). В противном случае — бесконечномерным. Базис векторного пространства - набор из максимального (для данногопространства) числа линейно независимых векторов. Следовательно, все остальные векторы пространства оказываются линейными комбинациями базисных. Если все базисные векторы взаимно ортогональны, а длина каждого из них равна единице, то базис называется ортонормированным. Единичный базисный вектор называют ортом (обозначается ei, где i — номер координаты). Каждый вектор пространства может быть представлен в виде линейной комбинации базисных векторов: a = ∑ aiei. Коэффициенты разложения ai однозначно определяют вектор a. Поэтому часто говорят, что n -мерный вектор — это упорядоченная совокупность n чисел {ai}. Размерность векторного пространства равна количеству векторов, составляющих его базис. Виды систем координат на плоскости. Уравнения связи декартовых и полярных координат. Примеры. Под системой координат на плоскости понимают способ, позволяющий численно описать положение точки плоскости. Виды систем: прямоугольная (декартова) система координат и полярная.
Полярная система координат задается т. О, называемой полюсом, лучом Ор, называемым полярной осью, и единичным вектором e того же направления, что и луч Ор. Возьмем на плоскости т. М, не совпадающую с О. Положение т. М определяется двумя числами: ее расстоянием r от полюса О и углом φ, образованным отрезком ОМ с полярной осью (отсчет углов ведется в направлении, противоположном движению часовой стрелки) (см. рис. 24). Числа r и φ называются полярными координатами т. М, пишут М(r; φ), при этом r называют полярным радиусом, φ — полярным углом. Для получения всех точек плоскости достаточно полярный угол φ ограничить промежутком (-; ] (или 0< φ < 2r), а полярный радиус — [0;∞). В этом случае каждой точке плоскости (кроме О) соответствует единственная пара чисел r и φ, и обратно. Установим связь между прямоугольными и полярными координатами. Для этого совместим полюс О с началом координат системы Оху, а полярную ось — с положительной полуосью Ох. Пусть x и у — прямоугольные координаты точки М, а r и φ — ее полярные координаты. Из рисунка 25 видно, что прямоугольные координаты точки М выражаются через полярные координаты точки
Полярные же координаты т. М выражаются через ее декартовы координаты (тот же рисунок) такими формулами
Определяя величину φ, следует установить (по знакам x и у) четверть, в которой лежит искомый угол, и учитывать, что - < φ< .
28. Прямая на плоскости. Виды задания прямой на плоскости. Взаимное расположение прямых на плоскости. Общее уравнение прямой на плоскости в декартовых координатах: Ах+Ву+С=0, где A, B и C — произвольные постоянные, причем A и B не равны 0 одновременно Способы задания прямой: 1)Задание с помощью зависимости у=у(х). 2)Параметрическое задание: х=х(t), у=у(t), где t-параметр. 3)Векторное задание r =r(t), где t- параметр. Прямые на плоскости: 1) у=kx+b – уравнение прямой с угловым коэффициентом k. 2)общее уравнение прямой Ах+Ву+С=0. 3) уравнение прямой, проходящей через данную точку в данном направлении: y-yo=k(x-xo). 4)уравнение прямой, проходящей через две точки: Частные случаи расположения прямой: 1)если прямая проходит через начало координат, то b=0; 2) если прямая параллельна оси Ох, то у=b; 3) если прямая параллельна оси Оу, то х=const.
29.Прямая на плоскости. Угол между прямыми. Условие параллельности и перпендикулярности. Общее уравнение прямой на плоскости в декартовых координатах: Ах+Ву+С=0, где A, B и C — произвольные постоянные, причем A и B не равны 0 одновременно. Угол между прямыми можно вычислить: I. Пусть прямые заданы с помощью ур-ий с угл. коэф. l1: y=k1x+b1; l2: y=k2x+b2 tg=(k2-k1)/(1+k2*k1) è1) если k1= k2, то прямые параллельны; 2)если k2k1= -1, то прямые перпендикулярны; 3)если k1≠k2, то прямые пересекаются II. Пусть прямые заданы с помощью общих уравнений:
tg=(А1В2-А2В1)/(А1А2-В1В2) è 1)если А1В2= А2В1, то прямые параллельны; 2) если А1/А2= В1/В2=С1/С2, то прямые совпадают; 3) если А1А2+В1В2=0, то прямые перпендикулярны; 4) если А1В2≠А2В1, то прямые пересекаются. 30.Прямая на плоскости. Угол между прямыми. Расстояние от точки до прямой. Общее уравнение прямой на плоскости в декартовых координатах: Ах+Ву+С=0. Угол между прямыми tg=(А1В2-А2В1)/(А1А2-В1В2) Уравнение прямой с угловым коэф. у=kx+b. Угол между прямыми tg=(k2-k1)/(1+k2*k1). Расстоянием от точки до прямой называется перпендикуляр опущенный из этой точки на данную прямую. Пусть точка М1(х1, у1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М1: Либо такая формула
31.Кривые второго порядка. Канонические уравнения, графики, определения. Кривая называется кривой (линией) второго порядка, если она определяется уравнением второй степени относительно текущих координат х и у, т.е. уравнением вида Аx2 + 2Вxy + Сy2 + 2Dx + 2Еy + F = 0. К кривым второго порядка относятся: окружность, эллипс, гипербола, парабола. 1) Окружностью радиуса R с центром в т. М0(х0;у0) наз-ся множество всех таких точек пл-ти М, что расстояние М0М всегда одно и то же и равно R. Каноническое уравнение (x – х0)2 + (y – у0)2 = R2 2) Эллипсом наз-ся множество всех точек на пл-ти, сумма расстояний от каждой из которых до двух данных точек этой пл-ти, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами. Канонич.ур-е эллипса
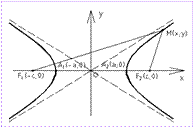
3) Гиперболой наз-ся множество всех точек пл-ти, модуль разности расстояний от каждой до двух данных точек пл-ти, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами. Канонич. ур-е гиперболы:
4) Параболой наз-ся множество всех точек пл-ти, каждая из которых одинаково удалена от данной точки, называемой фокусом и данной прямой, называемой директрисой. Расстояние от фокуса до директрисы наз-ся параметром параболы и обозн-ся р. Канонич. ур-е параболы у2=2рх (парабола симметрична оси Ох) х2=2ру (симметрична оси Оу) у2= -2рх (имеет фокус F(р/2;0) и директрису х= -р/2) х2= -2ру (имеет фокус F(0;р/2) и директрису у= -р/2
32.Плоскость в трехмерном пространстве. Виды задания пл-тей.
Виды: 1. Ур-ие плоскости проходящий через данную точку перпендикулярен заданному вектору. A(x-x̥)+ B(y-y̥)+ C(z-z̥)=0 2. Общее ур-ие плоскости Ax + By +Cz +D=0 Частные случаи: 1 D=0, пл-ть проходит через начало координат. 2 С=0, Oz и пл-ть параллельны 3 С= D=0 проходит через ось Oz 4 А=В=0 пл-ть параллельна пл-ти Oxy 5 А=В=D=0 пл-ть совпадает с пл-тью Oxy 3. Ур-ие пл-ти в отрезках x/a + y/b + z/c =1 нормальное ур-ие пл-ти xcos+ ycos + zcosµ –p=0
Угол между пл-тями. Q1:
Матрицы. Основные понятия. Виды матриц. Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины (или n столбцов одинаковой длины). Место каждого эл-та определяется номером строки и столбца, на пересечении кот. он находится. Эл-ты матрицы обозначаются aij, где i – ном. строки матр., а j – ном. столбца матр. У матрицы есть 2 диагонали. Элементы, стоящие на диагонали, идущей из верхнего угла, образуют главную диагональ матр., а эл-ты стоящие на другой диагонали образуют вспомогательную диагональ матр. Матрица записывается в виде:
Мат-ца может состоять как из одной строки, так и из одного столбца. Мат-ца может состоять даже из одного эл-та. Мат-цы равны между собой, если равны все соответствующие эл-ты этих матриц, т. е. А = В, если aij = bij. Мат-ца А наз. симметричной, если она квадратная и если все aij = аji. Если m = n, то мат-ца называется квадратной. Кв. мат-цу размера "n×n" называют матрицей n - ого порядка. Кв. мат-цу, у кот. все эл-ты, кроме эл-ов глав. диагонали, равны нулю, наз. диагональной матрицей. Диаг-ая матрица:
Диаг-ая матрица, у кот. каждый эл-т глав.диагонали =1, наз. единичной матрицей. Единичная матрица:
Кв. матрица, называется треугольной, если все эл-ты матрицы, расположенные по одну сторону от глав. диагонали, =0. Матрица, все эл-ты кот=0, наз. нулевой матрицей и обозначается буквой О. В матричном исчислении матрицы О и Е играют роль 0 и 1 в арифметике. Матрица, содержащая 1строку или 1столбец, наз. вектором (Или вектор-строка, или вектор-столбец). Матрицу В называют т р анспонированнойматрицей А, а переход от А к В транспонированием мат-цы, если эл-ты каждой строки матрицы А записать в том же порядке в столбцы матрицы В. Обозначается АТ.
Другими словами, aij = bji. Линейные операции над матрицами. Св-ва операций. Равенство матриц Матрицы A = || ai j || и B = || ai j || считаются равными, если они имеют одинаковые размеры и их соответствующие матричные элементы попарно равны:
К линейным операциям над эл-ми множества или пространства относятся оп-ции сложения эл-ов и их умножения на скаляр (число). Умножение матрицы на число
Сложение матриц Оп-ция сложения определена только для матриц одинаковых размеров. Результатом сложения матриц A = || ai j || и B = || bi j || явл. матрица C = || ci j ||, эл-ты кот. равны сумме соответствующих матричных эл-ов:
Линейной комбинацией матриц A и B наз.выражение вида
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 506; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.210.96 (0.174 с.) |







 , где
, где  и
и  – числовые коэфф-ты.
– числовые коэфф-ты.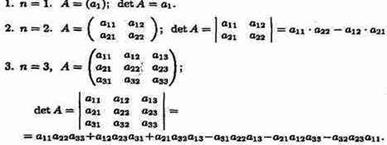


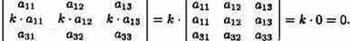

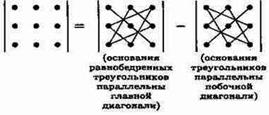

 -го порядка, определитель которой отличен от нуля. Если же определитель равен нулю, то такая матрица называется вырожденной.
-го порядка, определитель которой отличен от нуля. Если же определитель равен нулю, то такая матрица называется вырожденной.
 .
.

 применим алгоритм:
применим алгоритм:
 .
.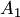 тоже образует систему: при
тоже образует систему: при  — линейно зависимую, а при
— линейно зависимую, а при 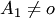 линейно независимую.
линейно независимую.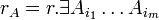 - столбцы, не входящие в БМ и они - максимальная линейно независимая система. ранг системы столбцов = m (число столбцов входящих в максимальную линейно независимую систему)
- столбцы, не входящие в БМ и они - максимальная линейно независимая система. ранг системы столбцов = m (число столбцов входящих в максимальную линейно независимую систему) 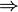 по утверждению 1 (если система линейно независима (количество k) и выражается через другую (количество l) то
по утверждению 1 (если система линейно независима (количество k) и выражается через другую (количество l) то 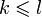 )
) 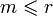 . по утверждению 1 и утверждению 2 (все максимальные линейно независимые системы состоят из одного и тогоже числа столбцов) и в силу того, что все столбцы линейно выражаются через столбцы максимальной линейно независимой системы
. по утверждению 1 и утверждению 2 (все максимальные линейно независимые системы состоят из одного и тогоже числа столбцов) и в силу того, что все столбцы линейно выражаются через столбцы максимальной линейно независимой системы 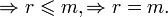
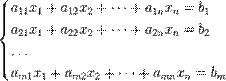
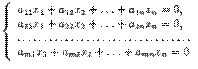 c1
c1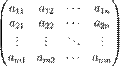
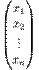
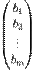 Ах=b
Ах=b Расширенной матрицей системы (А) называется матрица, получающаяся из исходной матрицы системы, присоединением вектора столбца свободных членов.
Расширенной матрицей системы (А) называется матрица, получающаяся из исходной матрицы системы, присоединением вектора столбца свободных членов.
 А= (А b)
А= (А b)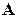 имеет обратную, то
имеет обратную, то 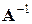 – квадратные одного порядка.
– квадратные одного порядка.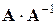 и
и 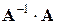 необходимо, чтобы матрицы
необходимо, чтобы матрицы 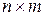 и
и 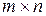 . Тогда матрица
. Тогда матрица 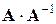 будет иметь размер
будет иметь размер 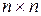 , а матрица
, а матрица 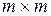 . Но для равенства
. Но для равенства 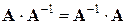 необходимо, чтобы размеры матриц
необходимо, чтобы размеры матриц 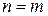 .
.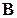 и
и 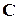 обладающие свойством
обладающие свойством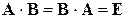 и
и 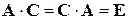 ,
,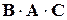 , причем
, причем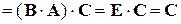
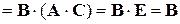 .
.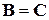 .
.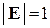 и для любых квадратных матриц
и для любых квадратных матриц 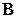
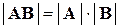 , то
, то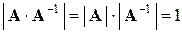
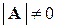 и
и 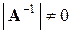 .
.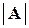 отличен от нуля. Причем обратная матрица
отличен от нуля. Причем обратная матрица 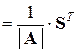 ,
,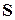 – матрица из алгебраических дополнений элементов матрицы
– матрица из алгебраических дополнений элементов матрицы 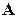 , т.е.
, т.е.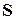
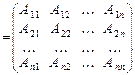 .
.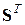 называется союзной (или присоединенной, или взаимной) для матрицы
называется союзной (или присоединенной, или взаимной) для матрицы 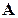 .
.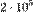 (200 000) тонн угля, а чёрной металлургии —
(200 000) тонн угля, а чёрной металлургии — 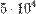 (50 000) тонн стали. Если каждая из них будет производить лишь
(50 000) тонн стали. Если каждая из них будет производить лишь 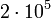 и
и 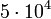 тонн, то часть продукции будет использоваться в другой отрасли.
тонн, то часть продукции будет использоваться в другой отрасли.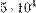 тонн стали требуется
тонн стали требуется 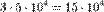 (150 000) тонн угля, а для производства
(150 000) тонн угля, а для производства 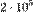 тонн угля нужно
тонн угля нужно 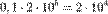 (20 000) тонн стали. Чистый выход будет равен:
(20 000) тонн стали. Чистый выход будет равен: 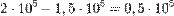 (50 000) тонн угля и
(50 000) тонн угля и 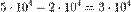 (30 000) тонн стали.
(30 000) тонн стали.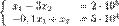

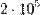 т угля, нужно умножить эти цифры на
т угля, нужно умножить эти цифры на  . Получим: (285714;28571).
. Получим: (285714;28571).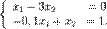
 т стали нужно: (214286; 71429).
т стали нужно: (214286; 71429).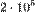 тонн угля и
тонн угля и 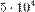 тонн стали: (285714 + 214286;28571 + 71429) = (500000;100000).
тонн стали: (285714 + 214286;28571 + 71429) = (500000;100000). Линейным (векторным) пространством называется множество Vпроизвольных элементов, названных векторами, в котором определены операции сложения и умножения вектора на число.
Линейным (векторным) пространством называется множество Vпроизвольных элементов, названных векторами, в котором определены операции сложения и умножения вектора на число. Сумма:U + V, U, V
Сумма:U + V, U, V  Vлинейные операции
Vлинейные операции , для любых
, для любых  (коммутативность сложения);
(коммутативность сложения);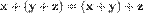 , для любых
, для любых  (ассоциативность сложения);
(ассоциативность сложения); , что
, что  для любого
для любого 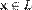 (существование нейтрального элемента относительно сложения), в частности L не пусто;
(существование нейтрального элемента относительно сложения), в частности L не пусто; существует такой элемент
существует такой элемент  , что
, что  (существование противоположного элемента относительно сложения).
(существование противоположного элемента относительно сложения). (ассоциативность умножения на скаляр);
(ассоциативность умножения на скаляр); (унитарность: умножение на нейтральный (по умножению) элемент поля P сохраняет вектор).
(унитарность: умножение на нейтральный (по умножению) элемент поля P сохраняет вектор). (дистрибутивность умножения на вектор относительно сложения скаляров);
(дистрибутивность умножения на вектор относительно сложения скаляров); (дистрибутивность умножения на скаляр относительно сложения векторов).
(дистрибутивность умножения на скаляр относительно сложения векторов).
 Прямоугольная система координат задается двумя взаимно перпендикулярными прямыми — осями, масштабом осей. Одну из осей называют осью абсцисс (осью Ох), другую — осью ординат (осью Оу).(рис.23). Единичные векторы осей обозначают i и j (| i |=| j |=1). Систему координат обозначают Оху, а плоскость, в которой она расположена, называют координатной плоскость. Рассмотрим произвольную т.М пл-ти Оху. Вектор ОМ называется радиусом-вектором т.М. Если ОМ=(x;y), то координаты т. Μ записывают так: М(х;у). Эти два числа x и y полностью определяют положение точки на плоскости.
Прямоугольная система координат задается двумя взаимно перпендикулярными прямыми — осями, масштабом осей. Одну из осей называют осью абсцисс (осью Ох), другую — осью ординат (осью Оу).(рис.23). Единичные векторы осей обозначают i и j (| i |=| j |=1). Систему координат обозначают Оху, а плоскость, в которой она расположена, называют координатной плоскость. Рассмотрим произвольную т.М пл-ти Оху. Вектор ОМ называется радиусом-вектором т.М. Если ОМ=(x;y), то координаты т. Μ записывают так: М(х;у). Эти два числа x и y полностью определяют положение точки на плоскости. следующим образом:
следующим образом: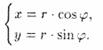
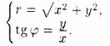
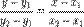 . Если х1=х2, то урав-е имеет вид х=х1. Если у1=у2 уравнение прямой примет вид у=у1. 5)уравнение прямой в отрезках
. Если х1=х2, то урав-е имеет вид х=х1. Если у1=у2 уравнение прямой примет вид у=у1. 5)уравнение прямой в отрезках 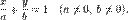 . 6)уравнение прямой, проходящей через данную точку, перпендикулярно данному вектору А(х-х0)+В(у-у0)=0.
. 6)уравнение прямой, проходящей через данную точку, перпендикулярно данному вектору А(х-х0)+В(у-у0)=0.
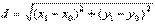 .
.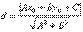

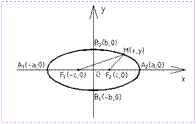


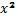 +
+  +
+ 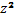 =1
=1 ,Q2:
,Q2: